In all but the smallest organizations, decisions of one sort or another are made at various levels and by many people.
Since every decision is partly a decision about risk, organizations delegate the responsibility for risk management and the authority to make risk decisions (for short, “delegate risk”) in the same way they delegate decision-making authority. That is through the organizational reporting structure of who reports to whom. That’s the same way budgets are parceled out to lower organizational units.
There are parallels between delegation of risk and delegation of budgets. In both cases, subsidiary managers are given some of the authority of the boss to make decisions, and bear the primary responsibility for the consequences of those decisions. But in both cases, the boss retains ultimate accountability for the consequences of her own and her subordinates’ decisions.
What’s different about delegation of risk is that the financial impacts (loss magnitudes) do not add up the way budgets do. If I have a divisional budget of $1 million, I might set department A’s budget at $400,000 and department B’s at $450,000, and reserve a budget of $150,000 for my headquarters operation. That’s a necessary mathematical equality.
But to see how the math of risk is a bit different, let’s take the hypothetical example of a CIO who has two data center directors reporting to him, one for the primary data center and one for the backup.
An Operational Risk Example
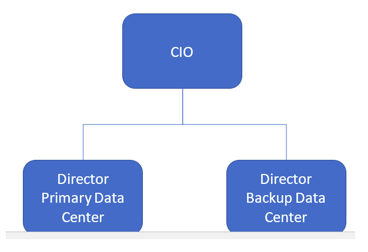Suppose the CIO and his two directors have collaborated on FAIR analyses of the distributions of potential losses for the two data centers for the coming fiscal year. They agree as follows:
- The primary data center may have losses between $0 and a maximum of $10M, with $75K being most likely.
- The backup data center may have losses between $0 and a maximum of $5M, with $25K being most likely. The backup data center is less-fully equipped and less stressed so its numbers are smaller.
- They judge the “most likely” values to have a medium level of confidence, and that losses in the two data centers will probably not have any common causes, so any losses will be statistically independent.
They model these loss magnitudes with PERT distributions and do a Monte Carlo simulation of a year of experience, and get the following simulated probability distributions for annual losses.
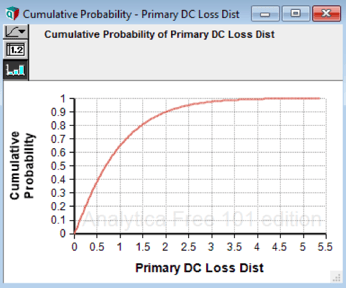
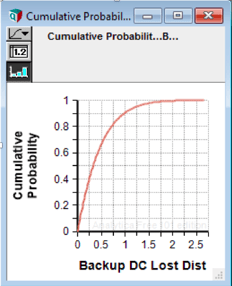
(Note that the loss scales are equal, so that $2.5M of loss is the same horizontal distance on both charts.)
The Director of the primary data center notes that she has a 90% chance that the loss for the primary data center will be $2M or less. Her colleague sees his 90% point for loss in the backup data center is $1M.
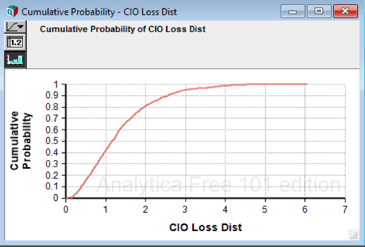
So the CIO’s 90% point for combined loss will be $3M, right?
Wrong!
The CIO does a Monte Carlo simulation that for each trial adds the losses of the two data centers. He finds that his 90% point is $2.5M, a good bit less than $3M. His loss distribution is shown on the same scale. The effect is even more pronounced at the 95% level, where the difference is $750K. However the means and medians do add, approximately, as do the maximums.
The CIO is getting the benefit of a portfolio effect, where the higher-than-average outcomes for the primary data center tend to be somewhat offset by the lower-than-average outcomes for the backup data center.
The conclusion is that the way that risk rolls up in the org chart is a bit different than the way that expenses do.
Still, $2.5M is a lot of money even for the CIO’s budget. And there is a good chance he will not need much of it. How should he treat that risk?
Together with the CFO, they decide to buy an insurance policy with a maximum payout of $2M, and self-insure for the deductible and any loss over $2M. Based on the analysis, and the fact that it survived multiple challenges from all the stakeholders, the CIO and CFO both feel comfortable that they understand the risk of loss in the data centers and have covered the risk prudently.
Program Risk Analysis
The same kind of thinking applies to program risk. Suppose I am bonused on an objective to reduce the unit cost of widgets. I have a bonus at risk if I fail.
I define a program to accomplish the goal, and I delegate responsibility for parts of the program to my managers. Adam has the goal to qualify and select a supplier for some new technology, and get the technology operational. Breanna has the goal to train the workforce on the new technology. Carol’s goal is to negotiate better terms for the raw materials.
Each of them can earn a bonus for achieving their goal, so each has some risk of failure and something to lose if they do. But I still own all their risk, plus my own risk for designing and managing the program. My boss owns the risk of my failure. And so on up the line, another example or risk being delegated in the organization.
What has this got to do with the FAIR model?
All the ideas and terminology of FAIR still apply. The loss magnitude is the loss of the bonuses to the individuals. To the company, the loss magnitude is the cost reductions not achieved if the program fails. The threats are all the factors that could prevent the program from succeeding. The thinking is the same as with cyber risk, showing once again the generality of the FAIR ontology. Risk appears in all human endeavors, and needs to be managed.
