Sometimes, the most mathematically oriented risk officers we meet ask this question: Is FAIR a Value-at-Risk (VaR) model? This happens mostly with risk officers who have extensive experience in credit risk, operational risk and market risk and who are first exposed to FAIR presented as a standard Cyber VaR model. (Learn more: What is a Cyber Value-at-Risk Model?)
In this article, we'll attempt to answer this question and address some of the most common sources of confusion.
Justin Theriot is a data scientist at RiskLens, the technical adviser to the FAIR Institute.
Mathematical structure provides the underlying information of abstract ideas. The FAIR risk model is structured to measure and manage information (and operational) risk with resemblances to Value at Risk.
However, this statement has led to confusion as VaR’s reputation is built on short-term probabilities using daily data on financial returns. While there are differences in data available between cybersecurity and finance, we need to look at the underlying mathematical structure of VaR to properly make a comparison.
We begin by looking at risk as defined and modeled under the Basel II Accords by the Basel Committee on Banking Supervision. Under the Basel II Accords, published in 2004, which superseded the 1988 Accords, one of the three concept pillars deals with the maintenance of regulatory capital calculated for the three major components of risk that banks face:
- credit risk,
- operational risk and
- market risk, with other risks being deemed not quantifiable.
Within operational risk there are three different approaches:
- basic indicator approach,
- standardization approach and
- internal measurement approach
The latter being a form of the advanced measurement approach (AMA). These methods increase in complexity, with AMA being the most advanced of the three. Under the AMA, banks are allowed to develop their own internal empirical model, with the Loss Distribution Approach (LDA) being the most common approach taken in the banking industry.
In the January, 2001, Consultative Document: Overview of the New Basel Accord, the Basel Committee on Banking Supervision established the internal measurement approach as, “an operational risk exposure indicator plus data representing the probability that a loss event occurs, and the losses given such events.”
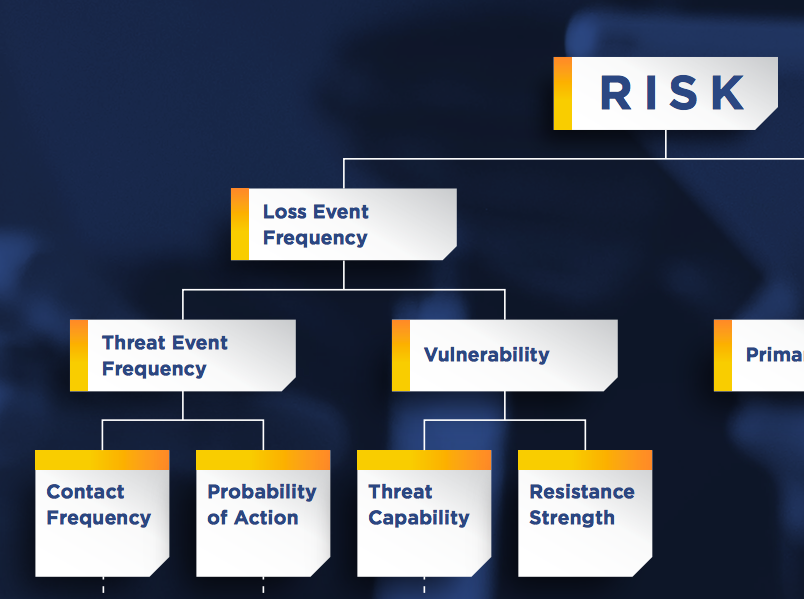
LDA expands on this approach by constructing a loss distribution that represents the expected total losses, a frequency distribution that describes the number of loss events and a severity distribution that describes the loss amount of a single loss event. The convolution of these functions (distributions) gives rise to the annual loss distribution. That's what FAIR does, as the model is used in conjunction with Monte Carlo simulations.
Within LDA, the output is a VaR type measurement. We must note there are different VaR calculations. Though within market risk, the variance-covariance with a Monte Carlo simulation is frequently the first VaR measurement used by a bank or financial institution. The method captures the diversification benefits of a multi-product portfolio due to the correlation coefficient matrix used in the calculation. Thus, if two stocks in a portfolio have a negative correlation, they move opposite to one another and the VaR would indicate a lower risk.
Regardless of where you start in the FAIR model, the mathematics works out the same as the common financial LDA approach thus negating any methodological differences.
| Download the FAIR model on one page |
Current cyber risk models use an aggregate method but as datasets become readily accessible, accuracy and precision will increase while the risk time-frame decreases from yearly outlooks, allowing FAIR to resemble the market risk VaR. Overall, FAIR closely mirrors LDA which is used to measure operational risk in financial institutions and banks. Even though FAIR and LDA are VaR type measurements, keep a mental note of the differences.
At a high level, when the FAIR risk model is used within cyber risk quantification solutions such as RiskLens that embed Monte Carlo simulations, you can still describe it at as a Cyber VaR model which should provide a useful reference point for executives or risk management officers who are otherwise familiar with VaR concepts. If your colleagues in Enterprise Risk Management want to dig in deeper, point them to the article on cyber VaR as well as to the FAIR book: Measuring and Managing Information Risk: a FAIR Approach.
